Initial state
1 2 3
4 5 6
_ 7 8
Goal state
1 2 3
4 5 6
7 8 _
We’ll solve it with A* using:
- Heuristic : Manhattan distance
Assume we generate moves in order: Up, Down, Left, Right.
Solving the 8-Puzzle Problem Using Manhattan Distance Heuristic
The 8-puzzle problem is a classic example used to explain heuristic search algorithms, especially A* search. In this blog, we will solve a simple 8-puzzle step by step using the Manhattan distance heuristic.
1. Problem Definition
Initial State (Current State)
1 2 3
4 5 6
_ 7 8
Goal State
1 2 3
4 5 6
7 8 _
Here, _ represents the blank tile, which can move up, down, left, or right.
Solution:
Search Strategy Used
We use the A* search algorithm, which evaluates each state using the function:
f(n)=g(n)+h(n)
Where:
- g(n) = cost from the initial state to the current state
- h(n) = heuristic estimate of the cost from the current state to the goal
- f(n) = total estimated cost
Heuristic Function: Manhattan Distance
Then:
Heuristic h(n) = Sum of Manhattan distances of all tiles (ignore the blank).
Step–by–step method
For each tile 1 to 8:
- Find its current row and column.
- Find its goal row and column.
- Compute:
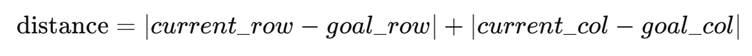
- Add this distance to a running total.
- Ignore the empty tile _.
At the end, that total = Manhattan heuristic value.
Current state:
1 2 3
4 5 6
_ 7 8
Goal state:
1 2 3
4 5 6
7 8 _
We will compute the Manhattan heuristic value h(n).
Step 1: Assign row and column numbers
We number rows and columns like this:
(0,0) (0,1) (0,2)
(1,0) (1,1) (1,2)
(2,0) (2,1) (2,2)
Step 2: Find positions of each tile
| Tile | Current Position | Goal Position |
| 1 | (0, 0) | (0, 0) |
| 2 | (0, 1) | (0, 1) |
| 3 | (0, 2) | (0, 2) |
| 4 | (1, 0) | (1, 0) |
| 5 | (1, 1) | (1, 1) |
| 6 | (1, 2) | (1, 2) |
| 7 | (2, 1) | (2, 0) |
| 8 | (2, 2) | (2, 1) |
| _ | (2, 0) | (2, 2) ← ignore blank |
Step 3: Apply Manhattan distance formula
The formula is:
Now calculate for each tile:
Tile 1
∣0−0∣+∣0−0∣=0
Tile 2
∣0−0∣+∣1−1∣=0
Tile 3
∣0−0∣+∣2−2∣=0
Tile 4
∣1−1∣+∣0−0∣=0
Tile 5
∣1−1∣+∣1−1∣=0
Tile 6
∣1−1∣+∣2−2∣=0
Tile 7
∣2−2∣+∣1−0∣=0+1=1
Tile 8
∣2−2∣+∣2−1∣=0+1=1
Step 4: Add all distances
h(n)=0+0+0+0+0+0+1+1=2
The Manhattan Distance heuristic value for:
1 2 3
4 5 6
_ 7 8
is:
h(n)=2
Define the Evaluation Function (A*)
A* search evaluates each state using:
f(n)=g(n)+h(n)
Where:
- g(n) = actual cost from the start state to the current state
- h(n) = heuristic estimate from the current state to the goal
- f(n) = total estimated cost
g(n)=0
Why g(n) = 0?
- No moves have been made yet
- This is the starting state
g(n)= 0
Evaluation function
f(n)=g(n)+h(n)=0+2=2
Generate Successor States
The blank tile _ is at position (2,0).
Possible moves:
- Move Right
- Move Up
Child State 1 — Blank Moves Right
New State
1 2 3
4 5 6
7 _ 8
Why g(n) = 1?
- One move has been made from the start
- Each move costs 1
g(n)=1
Manhattan Distance Calculation
Tile 7
∣2−2∣+∣0−0∣=0|2-2| + |0-0| = 0∣2−2∣+∣0−0∣=0
Tile 8
∣2−2∣+∣2−1∣=1|2-2| + |2-1| = 1∣2−2∣+∣2−1∣=1 h(n)=1h(n) = 1h(n)=1
Compute f(n)
f(n)=g(n)+h(n)=1+1=2
Child State 2 — Blank Moves Up
New State
1 2 3
_ 5 6
4 7 8
Why g(n) = 1?
- This state is also reached in one move
g(n)=1
Manhattan Distance Calculation
Tile 4
∣2−1∣+∣0−0∣=1
Tile 7
∣2−2∣+∣1−0∣=1
Tile 8
∣2−2∣+∣2−1∣=1
Compute f(n)
f(n)=1+3=4
Choose the Best State (A* Rule)
We select the state with the lowest f(n).
| State | g(n) | h(n) | f(n) |
| Right move | 1 | 1 | 2 |
| Up move | 1 | 3 | 4 |
✔ Selected State:
1 2 3
4 5 6
7 _ 8
Expand the Selected State
Blank tile position = (2,1)
Possible moves:
- Left → already visited (ignored)
- Up
- Right
Move Blank Right (Goal State)
New State
1 2 3
4 5 6
7 8 _
Evaluate Goal State
Why g(n) = 2?
- Two moves were made from the start
g(n)=2
Why h(n) = 0?
- All tiles are in their goal positions
h(n)=0
Evaluation function
f(n)=2+0=2
🎯 Goal state reached
Final Summary
- g(n) = number of moves already taken
- h(n) = estimated moves remaining (Manhattan distance)
- f(n) = total estimated solution cost
✔ Algorithm: A*
✔ Heuristic: Manhattan Distance
✔ Total moves: 2
✔ Solution: Optimal
One-Line Trick
g(n) counts steps taken, h(n) estimates steps left, f(n) decides the path.
