While constructing a decision tree using the CART algorithm, the dataset is split into
smaller subsets at each node.
After every split, the child nodes may contain samples belonging to a single class or multiple
classes.
Based on this, nodes in CART are classified as pure nodes or impure nodes.
The Gini Index is used to measure the purity or impurity of a node.
Gini Index in CART
Gini Index measures the probability of incorrect classification.
Formula:

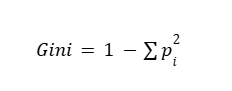
• Gini = 0 → Pure node
• Lower Gini → Better split
  The split with the minimum Gini Index is selected.
  Gini Index (CART)
  Given Data (same as earlier)
  From the table:
• Total samples = 9
• Y = 6, N = 3
  After splitting on the feature, we get two child nodes:
• C1 → 3Y / 3N
• C2 → 3Y / 0N

Step 1: Formula for Gini Index

Root node is IMPURE
Step 3: Gini Index for Child Node C1 (3Y / 3N)

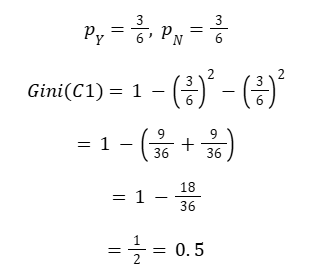
Maximum Gini impurity → Highly impure node
Step 4: Gini Index for Child Node C2 (3Y / 0N)

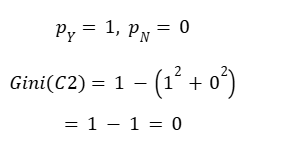
PURE node

Step 5: Interpretation (Pure vs Impure using Gini)

Node	Y	N	Gini Index	Type
Root	6	3	0.44	Impure
C1	3	3	0.5	Highly Impure
C2	3	0	0	Pure

Important Points
 Gini = 0 → Pure node
 Gini = 0.5 → Maximum impurity (binary class)
 CART selects the split with minimum weighted Gini
 Gini is faster to compute than entropy