So far, we have studied Simple Linear Regression, where the prediction depends on only one independent variable.
This works well in very simple situations.
But let us think about real life for a moment.
In real-world problems, we often have multiple features.
- A student may study for long hours, but without regular attendance and practice, marks may still suffer.
- A person may have many years of experience, but without the right skills or education, salary growth may be limited.
- A large house may exist, but without a good location or facilities, its price may not be high.
In short, outcomes are usually influenced by multiple factors at the same time.
This is why using only one independent variable is often not enough to make accurate predictions.
The Limitation of Simple Linear Regression
Simple Linear Regression:
- Uses only one input variable
- Cannot capture the effect of multiple factors together
To handle such situations, we need a more powerful model.
Moving to the Next Level
When the output depends on two or more independent variables, we extend simple linear regression into:
Multiple Linear Regression
The basic idea remains the same:
- Find a linear relationship
- Minimize prediction error
The only difference is:
- We now use multiple input variables instead of one
Now let us understand Multiple Linear Regression in detail.
Example:
- Predicting house price using:
- Area
- Number of bedrooms
- Location
Hypothesis Function for Multiple Linear Regression
When there are multiple features x1,x2,x3,…, the hypothesis function becomes:
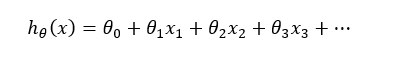

Meaning of Parameters
- Each θ value represents the importance (weight) of its feature
- Larger θ → feature has more influence on output
- θ₀ shifts the model up or down (intercept)
Gradient Descent in Multiple Linear Regression
In multiple linear regression:
- Cost function becomes a function of many parameters
- Graph becomes a multi-dimensional bowl
- Gradient descent still works the same way
Instead of a curve, we now move down a multi-dimensional surface
Global Minimum in Multiple Dimensions
- Even with many parameters, the cost function is convex
- There is only one global minimum
- Gradient descent is guaranteed to reach it
