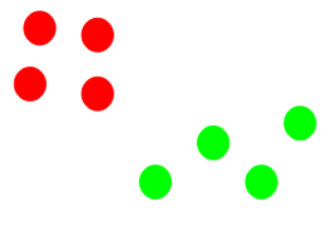
Suppose we have 8 data points on a graph.
Our goal is to group these points into clusters using the K-Means algorithm.

Step 1: Choose the Number of Clusters (K)

• First, we decide how many clusters we want.
• Let us choose K = 2, meaning:
  • We want to divide the 8 points into 2 groups.

👉 This value of K is chosen before running the algorithm.

Step 2: Select K Random Points as Initial Centroids

• Since K = 2, we randomly select 2 points from the dataset.
• These points act as the initial centroids.
• In the diagram:
  • One centroid is shown in red
  • The other centroid is shown in green

👉 At this stage, centroids may not be in the correct position. They are only a starting guess.

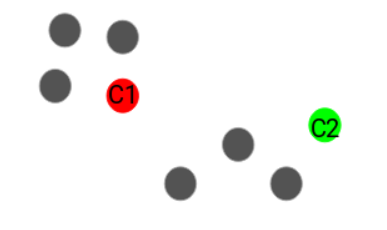
Step 3: Assign Each Point to the Nearest Centroid

• For each of the 8 data points:
  • Calculate the distance from the red centroid
  • Calculate the distance from the green centroid
• Assign the point to the cluster whose centroid is closest.

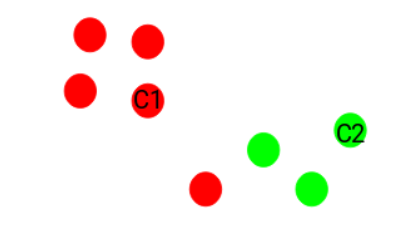
Result:

• Points closer to the red centroid → Red cluster
• Points closer to the green centroid → Green cluster

👉 This forms the first set of clusters.

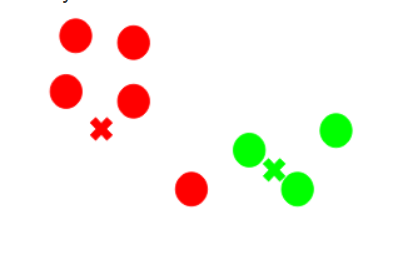
Step 4: Recompute the Centroids

• Now, for each cluster:
  • Take all points belonging to that cluster
  • Calculate their mean (average position)
• The mean position becomes the new centroid.

In the diagram:

• Red and green crosses represent the new centroids

👉 Centroids move toward the center of their respective clusters.

Step 5: Repeat Steps 3 and 4 (Iterations)

• Using the new centroids:
  • Again assign points to the nearest centroid
  • Again recompute the centroids

👉 One complete cycle of:

• Assigning points
• Updating centroids

is called one iteration.

This process is repeated multiple times.