What is MAE?
MAE measures the average magnitude of errors, without considering direction (positive or negative).
It answers:
“On average, how much is my model wrong?”
Formula
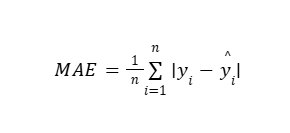
Where:
n= number of data points
yi= actual value
yi= predicted value
Delivery Prediction Example
What Is This Delivery Prediction Example?
Real-Life Problem
Food delivery apps (Zomato, Swiggy, Amazon, etc.) want to predict:
“How long will this order take to reach the customer?”
Inputs (Features)
- Distance to customer
- Traffic condition
- Restaurant preparation time
- Time of day
Output (Target)
- Delivery time (in days or hours)
This is a regression problem because:
- Output is a number, not a category
Why We Compare Actual vs Predicted?
After training:
- Model predicts delivery time
- Real delivery happens
- We know the actual delivery time
The difference tells us:
How good the learning was
What Is the Model “Learning” Here?
From multiple examples, the model learns:
- “Longer distance → more time”
- “Traffic → delay”
- “Peak hours → more delay”
Over time, errors reduce:
- Predictions become closer to actual values
That improvement = learning
In the delivery-time example, the model predicts:
How many days (or hours) a delivery will take
So:
- Output is a number
- Small mistakes are usually acceptable
- We want a simple and practical measure of error
Example: Predicting Delivery Time (in days)
| Order | Actual (days) | Predicted (days) | Absolute Error ∣Actual–Predicted∣ |
| 1 | 2.0 | 2.2 | ∣2.0−2.2∣=0.2 |
| 2 | 3.0 | 2.9 | ∣3.0−2.9∣=0.1 |
| 3 | 1.5 | 1.6 | ∣1.5−1.6∣=0.1 |
| 4 | 4.0 | 3.8 | ∣4.0−3.8∣=0.2 |
Step 2: Substitute Values from the Table
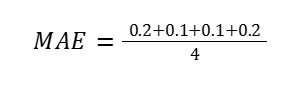
Step 3: Final Calculation
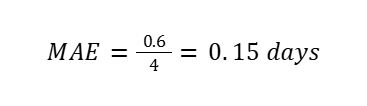
This tells us:
“On average, the delivery time prediction is wrong by 0.15 days.
Adding an Outlier to the Delivery Example
So far, we had these delivery errors:
Original Errors (Normal Cases)
| Delivery | Error (days) |
| 1 | 0.2 |
| 2 | 0.1 |
| 3 | 0.1 |
| 4 | 0.2 |
These are small, normal errors — the model is doing reasonably well.
Now Add an Outlier
What Are Outliers? (Very Important Concept)
Simple Definition
An outlier is a data point that is very different from most other data points.
In simple words:
A value that does not follow the normal pattern
Delivery-Time Outlier Example
Normally:
- Most deliveries take 2–4 days
But one order:
- Takes 10 days
Why?
- Heavy rain
- Road closure
- Strike
- Accident
That 10-day delivery is an outlier.
Why Are Outliers Important?
Outliers can:
- Distort averages
- Mislead model evaluation
- Make errors look larger than they usually are
Suppose one delivery was delayed heavily due to:
- heavy rain
- vehicle breakdown
- road closure
This delivery took much longer than expected.
Updated Errors (Including an Outlier)
Delivery Time Prediction – Including an Outlier
| Delivery | Actual Time (days) | Predicted Time (days) | Absolute Error ∣Actual–Predicted∣ |
| 1 | 2.0 | 2.2 | ∣2.0−2.2∣=0.2 |
| 2 | 3.0 | 2.9 | ∣3.0−2.9∣=0.1 |
| 3 | 1.5 | 1.6 | ∣1.5−1.6∣=0.1 |
| 4 | 4.0 | 3.8 | ∣4.0−3.8∣=0.2 |
| 5 | 5.0 | 8.0 | ∣5.0−8.0∣=3.0 🚨 Outlier |
Why is this an outlier?
Because its error (3.0 days) is much larger than all other errors.
What Happens to MAE Now?
Step-by-Step MAE Calculation
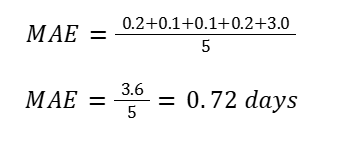
Interpretation
Earlier:
- MAE = 0.15 days (~3.6 hours)
After adding the outlier:
- MAE = 0.72 days (~17.3 hours)
What does this tell us?
- One extreme delivery increased the average error
- But MAE is still controlled
- The outlier does not completely dominate the metric
Why This Matters for Understanding Outliers
What Is an Outlier?
An outlier is a data point whose error is much larger than most other data points and does not follow the normal pattern.
Why MAE Handles Outliers Reasonably Well
- MAE treats all errors equally
- It does not square the error
- Large errors increase MAE, but do not explode it
This makes MAE suitable when:
- Outliers exist due to real-world issues
- We want to understand typical performance
Adding an outlier increases MAE, but MAE does not allow one extreme case to completely dominate the overall error.
Why This Makes Sense for Delivery Prediction
Reason 1: Simple to Understand
Delivery managers, customers, and business teams understand:
“Our prediction is off by 0.15 days on average”
Much easier than:
- Squared errors
- Complex math
Reason 2: All Errors Matter Equally
In delivery systems:
- 0.2-day error
- 0.1-day error
Both matter similarly.
MAE treats:
- All errors fairly
- No special punishment
Reason 3: Robust to Outliers
Sometimes:
- Most deliveries take 2–4 days
- One delivery takes 10 days (rain, accident, strike)
That rare case should not define overall system quality.
MAE:
- Includes the error
- But does not let it dominate
So MAE reflects typical performance, not rare events.
Reason 4: Same Unit as Output
Delivery time is measured in:
- Days or hours
MAE is also in:
- Days or hours
This makes interpretation very natural.
Advantages of MAE
1. Easy to Understand & Interpret
- MAE is expressed in the same unit as the output.
- Example:
- MAE = 0.15 days
- Means → predictions are off by 0.15 days on average
No complex math interpretation needed.
2. Treats All Errors Equally
- Every error contributes linearly.
- A 1-day error is treated twice as bad as a 0.5-day error (not four times).
This matches many real-world expectations.
3. Robust to Outliers
- Large errors do not dominate the metric.
- One extreme case (outlier) increases MAE but does not explode it.
Good when data naturally contains rare extreme events.
4. Suitable for Real-World Problems
- MAE reflects typical model performance.
- Preferred when average behavior matters more than rare worst cases.
5. Works Well for Business Communication
- Non-technical stakeholders easily understand:
“Our model is wrong by X units on average.”
Disadvantages of MAE
1. Does Not Penalize Large Errors Heavily
- A large error and multiple small errors can look similar.
- Example:
- One 5-day delay
- Five 1-day delays
→ MAE may treat both similarly
Not ideal when large errors are dangerous.
2. Less Sensitive to Extreme Mistakes
- MAE may hide serious failures if they are rare.
- Critical systems often need strong punishment for big errors.
3. Not Ideal for Optimization Theory
- MAE is not differentiable at zero.
- Some optimization algorithms prefer MSE/RMSE.
This is mostly a theoretical issue, not a practical one for beginners.
When Should We Use MAE?
Use MAE when:
✔ You want simple interpretation
✔ All errors matter equally
✔ Dataset contains outliers
✔ Typical performance is more important than worst-case
✔ Results need to be explained to non-technical users
When NOT to Use MAE?
Avoid MAE when:
Large errors are catastrophic
Worst-case performance matters most
Safety-critical systems are involved
In such cases, use RMSE.
Real-World Use Cases of MAE
1. Delivery Time Prediction
- Small delays are common
- Rare extreme delays should not dominate evaluation
MAE is preferred
2. House Price Prediction
- Typical error matters more than rare expensive houses
MAE gives realistic average error
3. Sales Forecasting
- Businesses want to know average forecast deviation
MAE is intuitive
4. Weather Prediction (Temperature)
- Small deviations are acceptable
- Extreme cases are rare
MAE reflects normal accuracy
5. Academic Performance Prediction
- Predicting marks, GPA, attendance
MAE is easy for educators to interpret
In the previous section, we used Mean Absolute Error (MAE) to measure the average prediction error. MAE treats all errors equally. However, in many real-world applications, large errors are far more dangerous than small ones. To address this limitation, we use Mean Squared Error (MSE).
Mean Squared Error (MSE)
Why Do We Need MSE?
MAE gives:
- Average error
- Equal weight to all mistakes
But consider:
- One prediction is wrong by 5 days
- Five predictions are wrong by 1 day
MAE treats both almost equally.
In real life:
- A single large mistake may be much worse.
MSE is designed to punish large errors more strongly.
