Classification metrics

Suppose I build a machine learning model.
It gives predictions.
How do I know if my model is GOOD or BAD?

• By checking accuracy
• By seeing correct predictions

Is being correct most of the time always enough?

Why Accuracy Alone Fails

Imagine a hospital uses an AI model to detect a serious disease.

• Total patients = 1000
• Actually sick = 10
• Healthy = 990

Model says:
 Everyone is healthy

How many predictions are correct?

• Correct = 990
• Accuracy = 99%

his model has 99% accuracy…
but it FAILED to detect even one sick patient.

So accuracy alone cannot tell us the full story.

High accuracy ≠ Good model

We don’t just want to know how many predictions were correct,
we want to know HOW the model is making mistakes.

This is why we need Classification Metrics.

WHY Classification Metrics Exist

Classification metrics help us:

• Measure model performance properly
• Understand different types of errors
• Decide whether the model is useful in real life”

Why We Need Classification Metrics

1. Accuracy alone can be misleading
2. Different mistakes have different impact
3. Some problems need confidence, some need coverage
4. Real-world decisions depend on error type

To evaluate any machine learning model,
we use something called Performance Metrics.

Performance metrics are numerical measures
that tell us how well a model is performing.

Performance Metrics = Model Evaluation Measures

For classification problems, we use classification performance metrics.

What Exactly Do Classification Metrics Measure?

Classification metrics do NOT only count correctness.

They measure:

• How many predictions were correct
• How many positives were detected
• How many false alarms occurred
• How many real cases were missed

Classification metrics analyze model errors in detail

Before calculating any metric,
we must first understand what kinds of predictions a model makes.

For that, we use something called the Confusion Matrix.

All classification performance metrics
are derived from the confusion matrix.

First we understand how predictions are classified
then we measure how good those classifications are.

When we build a classification model, its job is simple:

• Predict YES or NO
• Predict Spam or Not Spam
• Predict Sick or Healthy
• Predict Pass or Fail

Once predictions are made, a natural question arises:

How good is our classification model?

When we build a classification model, its job is simple:

• Predict YES or NO
• Predict Spam or Not Spam
• Predict Sick or Healthy
• Predict Pass or Fail

Once predictions are made, a natural question arises:

How good is our classification model?

But after predictions are made, a very important question arises:

How good is our model?

At first glance, the answer seems easy:

“Just check how many predictions are correct.”

This idea leads to accuracy

But this is where the problem starts.

---

Spam Filter Example (Very Important)

Suppose your spam filter checks 100 emails.

At first glance:

• 95 emails are classified correctly
• Accuracy = 95%

Sounds great, right?

Now think carefully.

---

Case 1: Most Emails Are Spam

Out of 100 emails:

• 90 are actually spam
• 10 are legitimate

Model prediction:

• Marks all 100 emails as spam

Result:

• Spam emails caught → 90 (correct)
• Important emails blocked → 10 (wrong)

Accuracy:

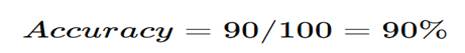
But ask yourself:

Would you use a spam filter that blocks important emails?

 No.

Case 2: Very Few Spam Emails (More Realistic)

Out of 100 emails:

• 5 are spam
• 95 are legitimate

Model prediction:

• Again marks all 100 as spam

Result:

• Correct = 5
• Wrong = 95

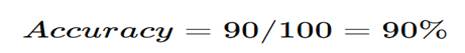
Now the model is clearly terrible.

What Did We Learn?

Accuracy only answers:

“How many predictions were correct?”

But it does NOT answer:

• What kind of mistakes were made
• Whether those mistakes are acceptable

So the real question is:

What type of mistakes is the model making?

This is why we need other classification metrics.

Confusion Matrix – The Foundation of All Metrics

Before calculating any metric, we must first understand how predictions are classified.

This is done using the Confusion Matrix.

What Is a Confusion Matrix?

A confusion matrix is a 2×2 table that compares:

• Actual values (ground truth)
• Predicted values (model output)

It shows all possible outcomes of classification.

The Four Outcomes

Prediction	Actual Positive	Actual Negative
Predicted Positive	True Positive (TP)	False Positive (FP)
Predicted Negative	False Negative (FN)	True Negative (TN)

Let’s understand each clearly:

• True Positive (TP)
  Model says YES, reality is YES
  Example: Sick person correctly identified
• True Negative (TN)
  Model says NO, reality is NO
  Example: Healthy person correctly cleared
• False Positive (FP)
  Model says YES, reality is NO
  Example: Healthy person marked sick (false alarm)
• False Negative (FN)
  Model says NO, reality is YES
  Example: Sick person marked healthy (dangerous)

Every classification metric is calculated using TP, FP, FN, and TN.

Accuracy – The Simplest Metric

What Is Accuracy?

Accuracy measures:

How many predictions were correct overall

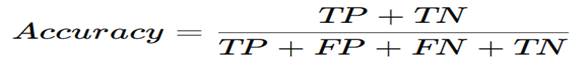
Example: Student Pass/Fail Prediction

• Total students = 100
• Correct predictions = 87

Accuracy = 87%

Meaning:

The model is correct 87% of the time.

When Accuracy Works Well

Accuracy is useful when:

• Dataset is balanced
• Both types of errors are equally serious

When Accuracy Lies 🚨

Fraud Detection Example

• 1000 transactions
• Only 10 are fraud
• Model predicts all as normal

Accuracy = 99%

But:

• Fraud detected = 0

A 99% accurate model that catches zero fraud is useless.

Precision

Problem: Restaurant Review Sentiment

Classes:

• Positive → YES
• Negative → NO

---

Step 1: What the MODEL Predicted

“Model predicts 80 reviews as POSITIVE”

So for these 80 reviews:

• Model said YES (Positive)

---

Step 2: What is the REALITY for These 80 Reviews

Out of these 80 predicted-positive reviews:

• 70 are actually Positive
• 10 are actually Negative

---

Step 3: Now Assign TP / FP / TN / FN

Case A: 70 reviews

• Predicted: Positive (YES)
• Actual: Positive (YES)

True Positive (TP = 70)

---

Case B: 10 reviews

• Predicted: Positive (YES)
• Actual: Negative (NO)

This is a False Positive (FP = 10)

 Why?

Because:

• Model said YES
• Reality was NO

This is a false alarm.

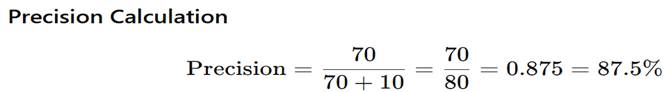
Interpretation (Very Important)

When the model says a review is Positive,
it is correct 87.5% of the time.

This means:

• The model’s positive predictions are mostly trustworthy
• Only a few false alarms exist

5. Another Numerical Example: Loan Approval (High-Risk Case)

Situation

A bank uses an ML model to approve loans.

Model Output

• Predicts 50 loan applications as Approved

Reality

• 40 applicants are actually good customers
• 10 applicants are risky and default later

So:

• TP = 40
• FP = 10

Precision

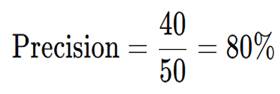
Meaning in Real Life

When the model approves a loan,
there is an 80% chance the customer is trustworthy.

The 20% false approvals can cause:

• Financial loss
• Legal trouble
• Reputation damage

That’s why precision is critical in loan approval systems.

Where Precision Matters Most (Very Important)

Precision is crucial when false positives are costly.

Examples:

• Spam filters
  Marking an important email as spam is dangerous
• Loan approval
  Approving a bad loan causes financial loss
• Product recommendations
  Showing irrelevant products annoys users
• Offensive content detection
  Flagging innocent posts can cause serious issues

 In all these cases:

It is better to say NO than to say YES incorrectly

100% Precision but Still a Bad Model

Step 1: Actual Situation (Reality)

Suppose we have 100 emails:

• 50 are actually spam
• 50 are legitimate

So there is a lot of spam in reality.

---

Step 2: Model’s Behaviour (Extreme & Lazy Model)

Now imagine a very conservative spam filter that behaves like this:

“I will mark an email as spam only if I am 100% sure.
Otherwise, I will say it is legitimate.”

So what does it do?

• It predicts ONLY 1 email as spam
• That email is actually spam

All other emails (99 emails):

• Are predicted as legitimate
• Even though many of them are spam

---

Step 3: Now Count TP, FP, FN, TN

For the ONE predicted spam email:

• Predicted: Spam
• Actual: Spam
   True Positive (TP = 1)

For predicted spam emails:

• No wrong spam predictions
   False Positive (FP = 0)

So far:

TP = 1

FP = 0

---

Step 4: Precision Calculation

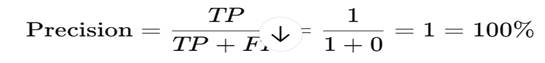
So mathematically:

Precision = 100%

And this is correct mathematically.

Then Why Is the Model BAD?

Because now look at what it MISSED.

Actual spam emails = 50

Spam detected = 1

So:

• 49 spam emails were missed
• Inbox is full of spam
• Users are unhappy

This means:

• Recall is extremely low
• Model is practically useless

Precision looks ONLY at predicted YES cases.
It completely ignores missed YES cases.

That’s why:

• Predicting very few YES → precision goes up
• But usefulness goes down

Precision answers:
“When the model says YES, is it correct?”

Precision is a classification metric that measures the correctness of positive predictions. It is defined as the ratio of true positives to the total number of predicted positives. Precision is important when false positive errors are costly.

Final Takeaway

• High precision → Few false alarms
• Precision focuses on quality, not coverage
• Precision alone can be misleading
• Must be used together with Recall

Precision tells us how reliable YES predictions are.
Now let us see Recall, which tells us how many real YES cases were found.

What Is Recall?

Recall tells us how many actual YES cases the model was able to detect.

More clearly:

Out of all the cases that were actually positive,
how many did the model correctly identify?

Recall focuses on:

• Coverage of positives
• Missed cases

---

3. Recall Formula (With Meaning)

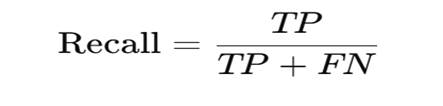
Where:

• TP (True Positive) = Actual YES, predicted YES
• FN (False Negative) = Actual YES, predicted NO (missed case)

So:

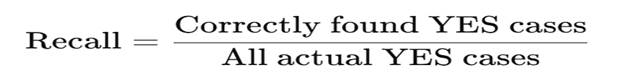
4. Numerical Example 1: Disease Detection (Classic Example)

Situation (Reality)

Suppose:

• 100 patients are actually sick

Model Prediction

• Model correctly identifies 85 sick patients
• Model misses 15 sick patients

So:

• TP = 85
• FN = 15

Recall Calculation

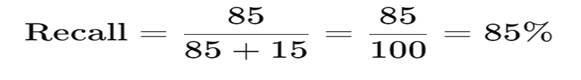
Interpretation (Very Important)

The model detects 85% of the sick patients
but misses 15%, who may not receive treatment.

In medical problems:

Missing a sick patient can be dangerous or fatal.

---

5. Numerical Example 2: Spam Filter (Easy to Visualize)

Reality

Out of 100 emails:

• 40 are actually spam
• 60 are legitimate

Model Prediction

• Correctly detects 30 spam emails
• Misses 10 spam emails (go to inbox)

So:

• TP = 30
• FN = 10

Recall Calculation

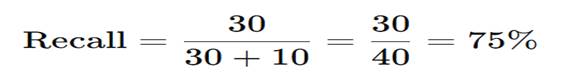
Meaning

The spam filter catches 75% of spam,
but 25% of spam still reaches the inbox.

Low recall here means:

• Users still see a lot of spam
• Spam filter is weak

7. Where Recall Matters the MOST (Critical Section)

Recall is crucial when missing a positive case is very dangerous.

Examples:

• Medical diagnosis
  Missing disease = patient suffers
• Cancer screening
  Missing cancer = life-threatening
• Fraud detection
  Missing fraud = financial loss
• Security systems
  Missing threats = safety risk

In such systems:

Better to raise some false alarms
than to miss real danger.

---

8. Problem With Only High Recall (Very Important)

Now comes the most important learning.

Extreme Case: 100% Recall but Still a Bad Model

Imagine a medical test that:

• Predicts EVERYONE as sick

Reality:

• 100 patients are sick
• 9,900 are healthy

Model prediction:

• All 10,000 predicted sick

So:

• TP = 100
• FN = 0

Recall

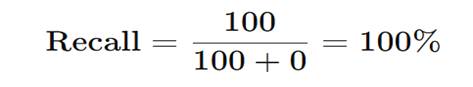
Perfect recall!

But what happened?

• 9,900 healthy people got false alarms
• Hospitals overflow
• Panic everywhere

So:

High recall alone does NOT mean a good model.

---

9. Why Recall Alone Is Not Enough

Recall does NOT tell us:

• How many false alarms occurred
• Whether YES predictions are trustworthy

So a model can:

• Catch all positives
• But still be unusable

That’s why recall must be balanced with Precision.

Out of all actual YES cases, how many did we find?

Recall is a classification metric that measures the ability of a model to identify all actual positive cases. It is defined as the ratio of true positives to the total number of actual positives. Recall is important when missing a positive case is costly or dangerous.

Final Takeaway

• High recall → Few missed cases
• Recall focuses on coverage, not accuracy of YES
• High recall alone can cause many false alarms
• Recall must be used with Precision

Precision tells us how reliable YES predictions are.
Recall tells us how many real YES cases were found.
Now let us combine both using F1-Score.

F1-Score – Balancing Precision and Recall

Why Do We Need F1-Score?

So far, we learned two important metrics:

• Precision → When the model says YES, is it correct?
• Recall → Did the model find all the YES cases?
• Now, the questions are:
•  What if a model has high precision but low recall?
   What if a model has high recall but low precision?

So we need ONE metric that:

• Considers both precision and recall
• Penalizes models that do well in only one
• Rewards balanced performance

This is why F1-Score exists.

What Is F1-Score? (In Simple Words)

F1-Score is a single number that tells how well a model balances precision and recall.

In other words:

A model gets a high F1-Score only if BOTH precision and recall are high.

If either one is low:

• F1-Score becomes low

F1-Score Formula

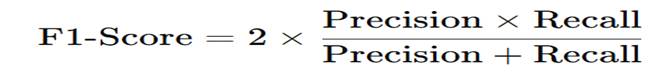
This is called the harmonic mean of precision and recall.

Numerical Example 1: Balanced Model (Good Case)

Model Performance

• Precision = 90%
• Recall = 80%

F1-Score Calculation

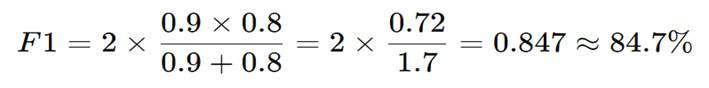
Interpretation

The model is reliable (high precision)
AND
The model covers most positives (good recall)

So the F1-Score is high.

Numerical Example 2: High Precision, Low Recall (Bad Case)

Model Performance

• Precision = 95%
• Recall = 10%

This happens when:

• Model predicts YES very rarely
• Almost never gives false alarms
• But misses most real cases

Simple Average (MISLEADING)

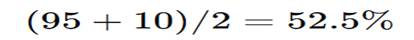
Looks okay… but it’s NOT.

F1-Score

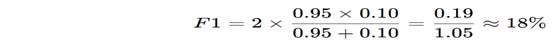
Interpretation

Even though precision is very high,
the model is terrible at finding real cases.

F1-Score exposes this clearly.

Numerical Example 3: High Recall, Low Precision (Also Bad)

Model Performance

• Precision = 20%
• Recall = 95%

This happens when:

• Model predicts almost everything as YES
• Catches nearly all positives
• But raises many false alarms

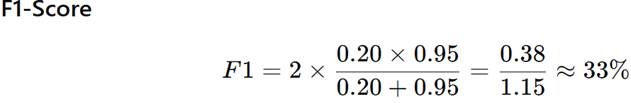
Interpretation

Catching everything is useless
if most predictions are wrong.

Again, F1-Score shows the truth.

hink of F1-Score like a balance scale:

• Precision on one side
• Recall on the other side

If one side is very low → balance breaks → low F1

Why Harmonic Mean Is Used (Very Important)

Simple Explanation

• Arithmetic mean allows cheating
• Harmonic mean does not

Example:

Precision	Recall	Average	F1
95%	10%	52.5%	18%
90%	90%	90%	90%

F1-Score punishes imbalance and rewards balance.

Where F1-Score Is MOST Useful

F1-Score is ideal when:

• Dataset is imbalanced
• Both false positives and false negatives matter
• You need one number to compare models

Common Uses:

• NLP (spam detection, hate speech)
• Medical screening (general assessment)
• Fraud detection
• ML competitions

---

10. Where F1-Score Is NOT Ideal

F1-Score may not be the best choice when:

• Only precision matters (e.g., loan approval)
• Only recall matters (e.g., cancer screening)

In such cases:

Focus on the more important metric directly

F1-Score answers:
“Is the model good at both being correct and not missing important cases?”

F1-Score is a classification metric that combines precision and recall using their harmonic mean. It provides a balanced evaluation of a model by penalizing extreme values of precision or recall. It is especially useful for imbalanced datasets.

Final Takeaway

• Precision alone can be misleading
• Recall alone can be misleading
• F1-Score balances both
• High F1-Score = truly good classification model

Metrics Comparison Table

Metric	Formula	What It Measures	Best Used When	Not Suitable When
Accuracy	(TP + TN) / All	Overall correctness	Balanced data	Imbalanced data
Precision	TP / (TP + FP)	Quality of YES predictions	False positives are costly	Missing positives is costly
Recall	TP / (TP + FN)	Coverage of actual positives	False negatives are dangerous	False alarms are costly
F1-Score	2PR / (P + R)	Balance of precision & recall	Both FP & FN matter	One metric is clearly more important

Summary

2. Accuracy – “How many predictions were correct?”

What Accuracy Tells Us

Accuracy measures:

Overall correctness of the model

It counts:

• Correct YES predictions
• Correct NO predictions

and ignores:

• Which class was more important

When Accuracy Is Good

Use accuracy when:

• Dataset is balanced
• Both types of errors are equally serious

Example:

• Student pass/fail prediction
• Balanced exam datasets

When Accuracy Fails

Accuracy is misleading when:

• One class dominates (95% NO, 5% YES)
• Errors have different costs

Key lesson:

High accuracy does NOT guarantee a good model.

---

3. Precision – “Can I trust YES predictions?”

What Precision Measures

Precision focuses on:

How correct the model’s YES predictions are

It answers:

“When the model says YES, is it right?”

When Precision Is Most Important

Use precision when:

• False positives are costly or harmful

Examples:

• Spam filters (don’t block real emails)
• Loan approval (don’t approve bad loans)
• Product recommendations (avoid irrelevant items)

When Precision Is Not Enough

Precision ignores:

• Missed positive cases

So:

• High precision does not mean high usefulness

Key lesson:

Precision = confidence in YES predictions.

---

4. Recall – “Did we find all the important cases?”

What Recall Measures

Recall focuses on:

How many actual YES cases the model found

It answers:

“Out of all real positives, how many did we catch?”

When Recall Is Critical

Use recall when:

• Missing a case is dangerous

Examples:

• Medical diagnosis
• Cancer screening
• Fraud detection
• Security systems

When Recall Alone Is Dangerous

Recall ignores:

• How many false alarms occurred

So:

• High recall can create panic and waste

 Key lesson:

Recall = coverage of important cases.

---

5. F1-Score – “Is the model balanced?”

What F1-Score Measures

F1-Score combines:

• Precision (quality)
• Recall (coverage)

It gives:

One balanced score

When F1-Score Is Best

Use F1-Score when:

• Dataset is imbalanced
• Both FP and FN matter
• You need a single comparison metric

Examples:

• Spam detection
• NLP tasks
• ML competitions

When F1-Score Is Not Ideal

Avoid F1-Score when:

• One metric is clearly more important
  (e.g., only recall matters in cancer screening)

 Key lesson:

F1-Score punishes imbalance and rewards balance.

---

6. Applications Summary

Application	Biggest Risk	Best Metric
Cancer detection	Missing disease	Recall
Spam filter	Blocking real emails	Precision
Loan approval	Approving risky customer	Precision
Fraud detection	Missing fraud	Recall
Recommendation system	Poor quality suggestions	Precision
General ML evaluation	Balanced performance	F1-Score