BFS uses a Queue to keep track of which nodes to explore next.
Definition
BFS explores all nodes level by level starting from the root.
It visits all nodes at depth 1, then depth 2, and so on.
Algorithm
- Put the start node in a queue (FIFO).
- While the queue is not empty:
- Remove the first node from the queue.
- If it is the goal, stop.
- Otherwise, expand it — generate all successors.
- Add those successors to the end of the queue (if not already visited).
- Repeat until goal is found or queue is empty.
Understanding BFS with the Given Diagram
A
/ \
B C
/ \ / \
D E F G
/ \
H I
What we are seeing
- The diagram shows a tree (or graph) with nodes labeled A to I.
- A is the Start (S) node.
- We are trying to find the Goal (I) node.
BFS Main Idea
BFS explores the tree level by level (breadth-wise), using a queue (FIFO).
It first visits all neighbors of the starting node before going deeper.
How it works step by step:
Step 1: Start at node A
- Start = A
- Put A in the queue.
- Queue = [A]
Now, remove A from the queue and explore its children → B and C.
After exploring A,
Queue = [B, C]
Step 2: Visit B
- Take B from the queue (FIFO → first in, first out).
- Explore B’s children: D and E.
Add them to the queue.
Queue = [C, D, E]
Step 3: Visit C
- Take C out of queue.
- Explore C’s children: F and G.
Add them to the queue.
Queue = [D, E, F, G]
Step 4: Visit D
- Take D out of queue.
- Explore its children: H and I.
Add them to the queue.
Queue = [E, F, G, H, I]
Step 5: Visit E
- Take E out of the queue (FIFO).
- Explore E’s children: (none).
- Nothing new to add.
- Queue = [F, G, H, I]
Step 6: Visit F
- Take F out of the queue.
- Explore F’s children: (none).
- Nothing new to add.
- Queue = [G, H, I]
Step 7: Visit G
- Take G out of the queue.
- Explore G’s children: (none) (G may be the goal — if so, BFS can stop here).
- If you continue for full traversal, nothing new to add.
- Queue = [H, I]
Step 8: Visit H
- Take H out of the queue.
- Explore H’s children: (none).
- Nothing new to add.
- Queue = [I]
Step 9: Visit I
- Take I out of the queue.
- Explore I’s children: (none).
- Nothing new to add.
- Queue becomes empty → BFS ends.
Order of Visiting:
A → B → C → D → E → F → G → H → I
That’s the exact order BFS explores — level by level, from left to right.
Time Complexity
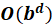
The O stands for “Order of”
- b → branching factor (how many children each node has)
- d → depth
- Depth (d) refers to the level in the tree (or search space)
- Example:
If each node has 2 children (b = 2) and depth = 3,
then →=8 nodes max.
Data Structure Used:
Queue (First-In-First-Out)
Properties
| Property | BFS |
| Completeness | Yes, if branching factor is finite |
| Optimality | Yes (if all step costs are equal) |
| Time Complexity | O(bᵈ) (b = branching factor, d = depth) |
| Space Complexity | O(bᵈ) (because all nodes stored in memory) |
| Type | Uninformed search |
Imagine you are exploring a city map —
you visit all places 1 km away first,
then all 2 km away, and so on — that’s BFS!
