Definition

DFS explores as far down a branch as possible before backtracking.
It follows one path deeply until it can’t go further, then goes back and explores other paths.

⚙️ Algorithm (Simple Steps)

1. Put the start node on a stack (LIFO).
2. While the stack is not empty:
   • Pop the top node.
   • If it is the goal, stop.
   • Otherwise, expand it.
   • Push all successors onto the top of the stack.
3. Repeat until goal is found or stack is empty.

Example

Using the same tree:

        A

       / \

      B   C

     / \  / \

    D  E F  G

   / \

  H   I

Step 1: Start at A

• Start from A (the root node).
• Push A onto the stack.
   Stack = [A]

Now pop A (take it out) and explore its children → B and C.
In DFS, we push right child first, so that the left child is explored first (LIFO).

 Stack = [C, B]

---

Step 2: Visit B

Pop B from the stack → visit it.

Explore B’s children → D and E
Push right child first (E), then left child (D).

 Stack = [C, E, D]

---

 Step 3: Visit D

Pop D (top of stack).

Explore D’s children → H and I.
Push I first, then H.

Stack = [C, E, I, H]

---

 Step 4: Visit H

Pop H (top of stack).
H has no children, so nothing is added.

 Stack = [C, E, I]

---

Step 5: Visit I

Pop I (top of stack).
I also has no children.

 Stack = [C, E]

---

 Step 6: Visit E

Pop E.
E has no children.

 Stack = [C]

---

Step 7: Visit C

Pop C.
C’s children = F and G.
Push G first, then F.

 Stack = [G, F]

---

Step 8: Visit F

Pop F, no children.
 Stack = [G]

---

 Step 9: Visit G

Pop G, no children.
Stack = []

---

Traversal Order (DFS Path):

 A → B → D → H → I → E → C → F → G

 Data Structure Used:

Stack (Last-In-First-Out)

Concepts

Property	DFS
Data Structure	Stack (LIFO)
Exploration Order	Deepest node first
Example Path	A → B → D → H → I → E → C → F → G
Time Complexity	O(bᵈ) (b = branching factor, d = depth)
Space Complexity	O(bd)
Complete?	No (can get stuck in infinite path)
Optimal?	No (may not find shortest path)

Properties

Property	DFS
Completeness	No (may get stuck in infinite paths)
Optimality	No
Time Complexity	O(bᵐ) (m = maximum depth)
Space Complexity	O(bm) (better than BFS)
Type	Uninformed search

Time Complexity of DFS

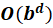
The O stands for “Order of”

• b → branching factor (how many children each node has)
• d → depth
• Depth (d) refers to the level in the tree (or search space)

d = maximum depth of the tree (how far down we go)

Meaning:

DFS explores all possible nodes along one path before backtracking.
So in the worst case, DFS might have to visit every node in the tree — all the way to depth d.

At each level:

• Level 0 → 1 node
• Level 1 → b nodes
• Level 2 → b² nodes
• …
• Level d → bᵈ nodes

Total ≈ 1 + b + b² + … + bᵈ ≈ O(bᵈ) (dominant term is bᵈ)

 Example:

If each node has 2 children (b = 2)
and the maximum depth = 3,

then the maximum nodes DFS may explore =

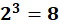
DFS keeps going deep into one branch before trying others.

So the time taken depends on:

1. How many children (b) each node can have, and
2. How deep (d) the tree can go.

If the tree is deep, DFS takes more time — because it must go down every possible path.

BFS vs DFS — Comparison Table

Feature	BFS	DFS
Strategy	Explore level by level	Explore deep along a branch
Data Structure	Queue (FIFO)	Stack (LIFO)
Completeness	Yes	No (for infinite depth)
Optimality	Yes (equal cost)	No
Time Complexity	O(bᵈ)	O(bᵐ)
Space Complexity	O(bᵈ)	O(bm)
Type of Search	Uninformed	Uninformed
Use When	You need shortest path	Memory is limited

Real-Life Analogy

Search	Analogy
BFS	Searching for a friend in a building by visiting every room on each floor before going to the next floor.
DFS	Searching by entering one room, exploring all its sub-rooms and closets deeply before moving to the next room.