The following diagram represents the structure of a single artificial neuron.

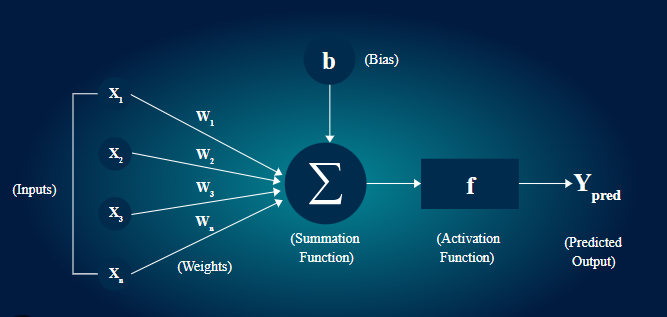
Each connection has a weight (importance), and the network learns by adjusting those weights .

An artificial neuron is the basic building block of a neural network.
It works similar to a biological neuron by taking input features, multiplying them with weights, adding a bias, and passing the result through an activation function to produce an output.
To understand how a neural network learns, we first study the working of a single artificial neuron using a simple example.

 Step-by-Step Explanation (Simple Version)

1️⃣ Input features
Tell them:

“Imagine we are trying to teach a neural network to recognize cats.
We give it three features:

• Has whiskers (1 = yes, 0 = no)
• Has pointy ears (1 = yes, 0 = no)
• Has fur (1 = yes, 0 = no)”

Example input:
[1, 1, 1] → means yes, it has whiskers, ears, and fur.

Neural Network Learning Example (Cat or Not Cat)

We’ll use:

• 3 input features
• 1 output neuron
• 1 training example

We want the network to learn whether an image is a cat (1) or not a cat (0).

Feature	Description	Value
x₁	Has whiskers	1
x₂	Has pointy ears	1
x₃	Has fur	1

2️⃣ Initialize weights randomly

Let the initial weights and bias be:

w₁ = 0.2,   w₂ = 0.3,   w₃ = 0.1,   bias = 0.1

3️⃣ Forward pass (prediction)

Compute weighted sum (z):

z=w1+w2+w3+bias

z=1×0.2+1×0.3+1×0.1+0.1=0.7

Now apply sigmoid activation to get a probability:

output=11+e-z=11+e-0.7≈0.668

So, the network says:

“This looks 66.8% like a cat.”

4️⃣ Compare with actual label

Actual answer = 1.
Predicted = 0.668.

Error=Target–Output=1-0.668=0.332

So, the network is off by 0.332 (33.2%).

5️⃣ Weight update (simple learning rule)(Backward pass)

We use a simple rule:

New weight=Old weight+Learning rateErrorInput

Let learning rate η = 0.1

Then:

w1=0.1×0.332×1=0.0332

w2=0.1×0.332×1=0.0332

w3=0.1×0.332×1=0.0332

b=0.1×0.332=0.0332

6️⃣ Update all weights

w1=0.2+0.0332=0.2332

w2=0.3+0.0332=0.3332

w3=0.1+0.0332=0.1332

b=0.1+0.0332=0.1332

7️⃣ Test again (after learning)

Now, compute again:

z=1×0.2332+1×0.3332+1×0.1332+0.1332=0.8328

Output=11+e-0.8328=0.6969

Now the network says:

“I’m 69.7% sure this is a cat (up from 66.8%)!”

Conclusion

Step	Output	Error
Before training	0.668	0.332
After 1 update	0.697	0.303

With more training examples, and many such updates, the network will keep adjusting until it predicts near 1.0 for cats and 0.0 for not-cats.

Key points

• Neural networks never know the correct answer at the start.
• The initial output is just a guess, based on initial random weights.
• Training (forward + backward propagation) is what improves the guess.

So yes, even though all features are “1,” the network outputs 0.668 instead of 1 — this is normal and expected.
It is not wrong, it just shows the network needs training.

From this example, we observe that a single artificial neuron learns by adjusting its weights and bias based on the error between predicted output and actual output.
Initially, the output is only a guess, but after training, the prediction improves.
Repeating this process with more training examples helps the neuron make accurate predictions.

Step-by-Step: How the Learning Happens in Single Artificial neuron

1. Input Stage (Getting the Data)
   Everything starts when we feed input data into the network.
   Each input is multiplied by a weight — a number that shows how important that input is.
   For example, if “hours studied” is more important than “hours slept,” it will have a higher weight.
2. Summation (Mixing the Inputs)
   The neuron adds up all the weighted inputs — kind of like combining ingredients in a recipe .
   Each neuron decides what to do with that mix next.
3. Activation Function (Decision Time!)
   Now comes the activation function, which decides whether the neuron should “fire” (activate) or stay quiet.
   It’s like a switch that says, “Yes, this pattern looks important — pass it on!”
4. Output (Making a Prediction)
   The final layer gives the network’s prediction — it could be “Pass” or “Fail,” “Cat” or “Dog,” “Spam” or “Not Spam.”
5. Error Calculation (Oops! That’s Wrong 😅)
   The network then compares its output with the correct answer.
   The difference between them is called Error.
6. Backpropagation (Learning from Mistakes)
   This is the magical part! 🪄
   The network sends the error backward through all the layers and adjusts the weights.
   The next time it makes a slightly better guess.
   Over many rounds (called epochs), the network becomes smarter and more accurate.

---

In Short

A Neuron learns by repeating three steps:
Guess → Check → Correct.
This simple cycle is the heart of deep learning!