Root Mean Squared Error (RMSE)

In the previous section, we discussed Mean Squared Error (MSE). Although MSE is mathematically useful, its squared units make it difficult to interpret. To overcome this limitation while keeping the advantage of penalizing large errors, we use Root Mean Squared Error (RMSE).

What is RMSE?

Root Mean Squared Error (RMSE) is the square root of Mean Squared Error.

RMSE measures the average prediction error while giving extra importance to large mistakes, and it expresses the error in the original unit of the target variable.

In short:

MSE → good for math
RMSE → good for humans

RMSE Formula

Where:

yi= actual value
yi= predicted value
n= number of observations

Step-by-Step Numerical Example (Delivery Time)

Dataset (Including an Outlier)

Delivery	Actual (days)	Predicted (days)	Error	Squared Error
1	2.0	2.2	0.2	0.04
2	3.0	2.9	0.1	0.01
3	1.5	1.6	0.1	0.01
4	4.0	3.8	0.2	0.04
5	5.0	8.0	3.0	9.00 🚨

Step 1: Compute MSE

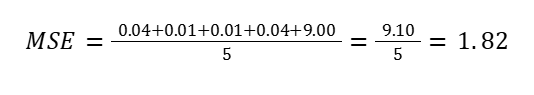
step 2: Take Square Root

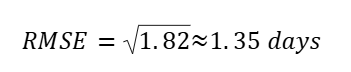
Interpretation of RMSE

RMSE = 1.35 days means that, on average, the model’s predicted delivery time deviates from the actual delivery time by about 1.35 days, with large delays having a strong influence.

Compare this with MAE:

MAE showed typical error
RMSE highlights serious mistakes

Why Taking Square Root Is Important

Problem with MSE

Units are squared (days²)
Hard to interpret

RMSE Solution

Square root cancels squared unit
Final unit = days

This makes RMSE:

Mathematically strong and human-readable

Advantages of RMSE — Explained Clearly

Penalizes Large Errors Strongly

Why is this an advantage?

Squaring makes big errors much larger
Taking root does not remove the penalty effect

Example:

Error = 0.2 → small impact
Error = 3.0 → dominates RMSE

This ensures:

Models with dangerous mistakes are clearly identified

More Interpretable Than MSE

Why is this an advantage?

RMSE is in the same unit as output
Humans understand days, marks, rupees—not squared units

Example:

RMSE = 1.35 days → meaningful
MSE = 1.82 days² → confusing

Widely Accepted Standard Metric

Why is this important?

Used in research papers
Used in industry
Default metric in many tools

Students will see RMSE again and again.

Useful for Risk-Sensitive Applications

Why?

Because:

One extreme mistake can cause big loss
RMSE exposes such risks

Example:

Medical dosage
Engineering loads
Financial risk

Disadvantages of RMSE — Explained Clearly

Highly Sensitive to Outliers

Why is this a disadvantage?

One rare extreme case can inflate RMSE
Typical performance may look worse than reality

Example:

One flood-delayed delivery affects entire score

Can Be Misleading for Average Performance

Why?

RMSE focuses on worst errors
Average daily performance may actually be good

Businesses may panic unnecessarily.

Harder to Explain Than MAE

Why?

Involves squaring and square root
Non-technical users prefer MAE

RMSE is better for engineers than managers.

When Should We Use RMSE?

Use RMSE when:

✔ Large errors are dangerous
✔ Worst-case performance matters
✔ Safety or cost is critical
✔ You want to detect serious failures

When Should We Avoid RMSE?

Avoid RMSE when:

Outliers are frequent and unavoidable
Typical performance matters more
Simple explanation is required

Use MAE instead.

RMSE measures average prediction error while strongly penalizing large mistakes and expressing the result in original units, making it ideal for applications where big errors are costly.

Compare RMSE with a Baseline Model (Most Important)

What is a baseline?

A simple model that predicts:

Mean of the target variable

Example:

Model	RMSE
Baseline (mean prediction)	2.8
ML Model	1.35

Since:

1.35<2.81.35 < 2.81.35<2.8

The ML model is clearly better.

A model is good if it beats the baseline.

Method 3: Compare RMSE Across Multiple Models

You usually train many models, not just one.

Model	RMSE
Linear Regression	1.9
Decision Tree	1.6
Random Forest	1.35

The lowest RMSE wins.

RMSE is mainly used for model comparison, not absolute judgment.