Mean Squared Error (MSE) calculates the average of squared differences between actual and predicted values.
By squaring the error, MSE gives more importance to large mistakes.
MSE Formula
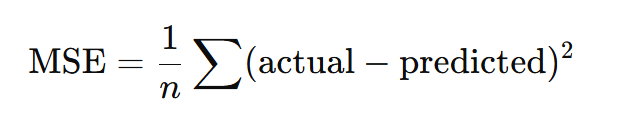
- Where:
- yi= actual value
- yi= predicted value
n= number of observations
Step-by-Step Numerical Example (Delivery Time)
Dataset (Including an Outlier)
| Delivery | Actual (days) | Predicted (days) | Error | Squared Error |
| 1 | 2.0 | 2.2 | 0.2 | 0.04 |
| 2 | 3.0 | 2.9 | 0.1 | 0.01 |
| 3 | 1.5 | 1.6 | 0.1 | 0.01 |
| 4 | 4.0 | 3.8 | 0.2 | 0.04 |
| 5 | 5.0 | 8.0 | 3.0 | 9.00 🚨 |
Step 1: Square Each Error
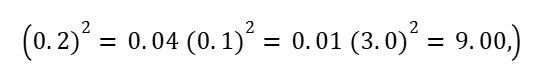
Step 2: Take the Mean

Interpretation of MSE
An MSE of 1.82 indicates that the model has large squared errors, mainly due to the extreme outlier.
Notice:
- Normal errors contribute very little
- Large error dominates the MSE
Why Is Squaring Important?
Squaring:
- Removes negative sign
- Amplifies large errors
| Error | Absolute | Squared |
| 0.1 | 0.1 | 0.01 |
| 0.5 | 0.5 | 0.25 |
| 3.0 | 3.0 | 9.00 |
A 3-day error becomes 9 times worse.
Advantages of MSE — Explained Simply
Strongly Penalizes Large Errors
Why is this an advantage?
What happens in MSE?
In MSE, we square the error:
Error=3⇒Squared Error=9\text{Error} = 3 \Rightarrow \text{Squared Error} = 9Error=3⇒Squared Error=9
So:
- Small error → stays small
- Large error → becomes very large
Why is this good?
Because in many real-life systems:
- One big mistake is much worse than many small mistakes
Example (Medical Dosage):
- Predict 1 mg wrong → small issue
- Predict 10 mg wrong → dangerous
MSE makes sure:
Big mistakes get extra punishment
Student intuition:
Think of a strict teacher:
- Small mistake → few marks lost
- Big mistake → heavy penalty
MSE = strict teacher
Mathematically Convenient
Why is this an advantage?
What does “mathematically convenient” mean?
It means:
- Easy to use in equations
- Easy to optimize
- Easy for computers to minimize
Differentiable Everywhere (Simple Meaning)
- Squared function is smooth
- No sharp corners
- Gradient can be calculated easily
Why this matters:
- ML models learn by gradient descent
- Gradient descent needs smooth curves
Why MAE is harder for training?
MAE uses:
∣y−y^∣
This has a sharp corner at 0 → difficult for calculus
📌 So during training:
Models prefer MSE
Student analogy:
- Smooth road → easy driving (MSE)
- Road with sudden turns → hard driving (MAE)
Encourages Stable Models
Why does MSE encourage stability?
What is instability?
A model that:
- Works well most of the time
- Occasionally fails very badly
How MSE fixes this?
Because:
- One extreme error increases MSE a lot
- Model is forced to reduce worst-case errors
This results in:
- More consistent predictions
- Fewer extreme failures
Example:
A delivery model:
- 95% deliveries → accurate
- 5% deliveries → very wrong
MSE highlights that 5% strongly.
Disadvantages of MSE — Explained Simply
Units Are Squared
Why is this a disadvantage?
What happens to units?
| Original | MSE Unit |
| Days | Days² |
| Marks | Marks² |
| Rupees | Rupees² |
Humans don’t think in:
- Days²
- Rupees²
Why is this confusing?
If:
- MSE = 4 days²
Students ask:
“What does 4 days² mean in real life?”
That’s why:
MSE is not intuitive
Solution:
Take square root → RMSE
Highly Sensitive to Outliers
Why is this a problem?
What is an outlier?
- Rare
- Unusual
- Extreme value
What happens in MSE?
Example:
- Normal error = 0.2 → squared = 0.04
- Outlier error = 3.0 → squared = 9.00
One outlier dominates the entire MSE.
Why is this bad?
Because:
- Model may look terrible due to one rare event
- Typical performance is hidden
Example:
Delivery delay due to:
- Flood
- Strike
- Accident
These are not model’s fault.
Not Intuitive for Humans
Why is this a disadvantage?
Humans think in averages, not squares
People understand:
- “Average error is 3 hours”
Not: - “Average squared error is 9 hours²”
Business communication problem
Try telling a manager:
“Our MSE is 2.3 rupees²”
They will ask:
“So… is that good or bad?”
MAE or RMSE communicate better.
| Aspect | Why Advantage | Why Disadvantage |
| Squaring errors | Punishes big mistakes | Outliers dominate |
| Mathematical form | Easy optimization | Hard interpretation |
| Stability | Reduces extreme failures | Hides typical behavior |
| Units | Useful in training | Meaningless for humans |
How to Judge Whether an MSE Is Good (Correct Way)
Method 1: Compare with a Baseline Model (Most Important)
How to Judge Whether an MSE Is Good (Correct Way)
Method 1: Compare with a Baseline Model (Most Important)
Create a simple baseline model, for example:
- Predict the mean of the target variable
Mean Baseline Model (Most Important)
This is the most widely used baseline.
The model predicts:
The average (mean) of the target variable for every input
Example: Delivery Time Prediction
Actual delivery times (days):
Example: Delivery Time Prediction
Actual delivery times (days):
2, 3, 1.5, 4, 5
Step 1: Calculate Mean
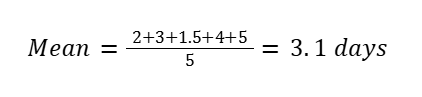
Step 2: Baseline Prediction
The baseline model predicts:
3.1 days for every delivery
No matter:
- distance
- traffic
- weather
Step 3: Compare Errors
Now calculate MSE or MAE for:
- Baseline model
- Your ML model
If:
- ML model MSE < Baseline MSE → model is learning
ML model MSE ≥ Baseline MSE → model is useless
Means
Create a simple baseline model, for example:
- Predict the mean of the target variable
Then compare:
| Model | MSE |
| Baseline model | 4.5 |
| Your ML model | 1.8 |
Since 1.8 < 4.5, your model is good.
A model is good if its MSE is much lower than the baseline.
